By cutting a circle into sectors and rearranging them,
you can see that the area of a circle resembles the area
of a parallelogram. The base of the parallelogram is
same as one-half the circumference of the circle, and the
height of the parallelogram is the same as the radius
the circle.
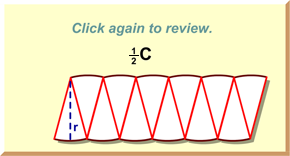
A = b · h
A = \(\frac{1}{2}\)C · r
A = \(\frac{1}{2}\) (2πr)·r
A = π ·r2

